 XonGrid Interpolation Add-in
XonGrid Interpolation Add-in
XonGrid is a free Excel library of functions to perform 1D, 2D, 3D, 4D and arbitrary dimension (ND) interpolations from scattered data. [ cette page en français ]
↓↓ DOWNLOAD XonGrid 4 for Excel 32 / 64 bits ↓↓
↓↓ DOWNLOAD XonGrid 4 sources ↓↓
Features
- Multivariate interpolation from scattered data
- Various interpolation methods: Linear, Akima, Bilinear, Nearest-neighbor, Natural-neighbors and Kriging
- 2D Cubic Spline Approximation
- Gaussian Process Regression
- Scaling of non-homogeneous parameters
- Array Formulas to speed up multiples interpolation
- Support for missing values and errors
- User defined interpolation
- Visual Basic Interface
Screenshots!

1D Interpolation Input

Interpolation Example

2D Example
Install the Add-in
Download and extract the XonGrid archive, open the add-in loader called INSTALL-XLL and click on the «Install xll» button. XonGrid is a user add-in, no administrative privilege is required to install it.
Macros must be activated to use the add-in loader. If you are not able to activate macros, follow these instructions to load the add-in in Excel. For the 32 bits version of Excel select XonGrid.xll and for the 64 bits version of Excel select XonGrid-w64.xll.
Use the Add-in
To use an interpolation function, click on the fx button on the formula bar, select the XonGrid 4 interpolation category, select a function then enter your data.
Examples of usage are included with the XonGrid archive.
Interpolation Functions
Available interpolation functions and options are presented on the table below. The Kriging interpolation with Method = 1.5 is highly recommended. Click on links for functions definition.
| Function Name |
Scaling of Parameters |
Linear Interpolation |
Akima Interpolation |
Natural Neighbors Interpolation |
Nearest Neighbor Interpolation |
Kriging Interpolation |
|---|---|---|---|---|---|---|
| Interp1d |  Not Applicable |
 Method = −1 |
 Method = −2 |
 Not Available |
 Method = 0 |
 Method = 1 to 1.99 |
| Interp2dTab |  Scaling = 0 or 1 |
 Not Available |
 Method = −3 |
|||
| Interp2d |  Not Available |
|||||
| Interp3d |  Not Available |
|||||
| Interp4d | ||||||
| InterpNd | See function description for details | |||||
Scaling of Parameters (Scaling = 0 or 1)
In an Euclidean space, the distance between two points A and B is given by:

Distance if Scaling = 0
If parameters are non-homogeneous physical variables (e.g. Volts and kg), calculate the distance without Scaling has no meaning. If Scaling = 1, XonGrid calculate the distance with scaled parameters and the transform shown below is applied to each parameter.

Initial parameters space (Scaling = 0) → Scaled parameters space (Scaling = 1)
The distance in the scaled space is:

Distance if Scaling = 1
Interpolation Methods
1D Linear Interpolation (Method = −1)
XonGrid considers a linear variation of the function between known values.
1D Akima Interpolation (Method = −2)
XonGrid use the Akima interpolation method. [ Akima's original article ]
2D Bilinear Interpolation (Method = −1)
XonGrid performs a bilinear interpolation from tabulated data.
2D Natural-neighbors Interpolation (Method = −3)
Xongrid call the nn implementation of natural-neighbor interpolation.
Nearest-neighbor Interpolation (Method = 0)
XonGrid returns the function value of the nearest-neighbor.
Kriging interpolation (1 ≤ Method ≤ 1.99)
XonGrid uses Ordinary Kriging interpolation with the power variogram presented below.
with 1 ≤ β ≤ 1.99 (β = 1.5 is a good choice)
Kriging interpolation on a large data set requires a huge amount of memory. To prevent Excel instabilities, the number of points is limited to 1024. Use the SubKriging optional parameter to perform a Kriging interpolation with more than 1024 points:
- If SubKriging is positive, SubKriging is the number of nearest points to select (1+nDim ≤ SubKriging ≤ 1024, SubKriging = 256 is a good choice)
- If SubKriging is negative, −SubKriging is the distance for selection of nearest points (SubKriging < 0)

Subset selection with SubKriging = 6 or SubKriging = −R
If the SubKriging parameter is missing, all points will be used for Kriging interpolation.
If Scaling = 1, the distance for selection of nearest points is calculated in the scaled space (see «Scaling of Parameters» section)
User defined Interpolation (Method = 100)
A user defined interpolation method can be implemented in the source/user-defined.c file of the source code. The build procedure is detailed in the README file.
Visual Basic Interface
Two XonGrid interpolation functions can be called from Visual Basic:
- interp_nd: ND interpolation from raw data
- interp_2d_tab: 2D interpolation from tabulated data
The declaration of these functions and three examples of usage are given in the Example-VB file.
Approximation and Regression Functions
These functions do not always honor the data. They provide a smoothed or approximated estimation of the function. Several parameters are available to control the smoothness of the output.
ND Gaussian Process Regression
Gaussian Process Regression is an other name of Kriging. The present implementation is more sophisticated than the one used for interpolation. The following functions are available:
- GpRegressNd Perform the Gaussian Process Regression
- GpStatsNd Return the empirical variogram and associated statistics
- GpVariogram Calculate the chosen variogram
For an introduction to Gaussian Process Regression, you can read the following sections of Numerical Recipes:
- 3.7.4 Interpolation by Kriging, p. 144
- 15.9 Gaussian Process Regression, p. 836
The guest access to Numerical Recipes is limited to few dozen of pages per month.
Examples of usage are given in the Example-gpr file.
2D Cubic Spline Approximation
XonGrid use the csa implementation of the cubic spline approximation technique. Two functions are available:
- CsApprox2d For 2D raw data
- CsApprox2dTab For 2D tabulated data
Examples of usage are given in the Example-csa file.
Build from Source
Download the source code, extract the archive and follow instructions in the README file.
Acknowledgements
XonGrid includes the following components:
FAQ
Is it free ?
Yes. XonGrid is a free software. Read the license for details. Nevertheless if you have found XonGrid really useful, I accept thanks at this address.
Interpolation is slow !
If you are performing multiple interpolation from the same data set, you should try array formulas as shown on example files. The table below shows calculations speed up for various Kriging (β = 1.5) interpolation cases.
| Interpolation function |
Number of data points |
Number of interpolated values |
Calculation time with single cell formula (s) |
Calculation time with array formula (s) |
Calculation speed up |
|---|---|---|---|---|---|
| Interp1d | 12 | 46 | 0.02 | 0.006 | 3 |
| Interp1d | 1000 | 46 | 23 | 0.5 | 46 |
| Interp2d | 16 | 256 | 0.14 | 0.025 | 6 |
| Interp3d | 64 | 256 | 0.56 | 0.03 | 19 |
| Interp4d | 192 | 256 | 0.9 | 0.05 | 18 |
| InterpNd (N=2) | 121 | 121 | 0.57 | 0.021 | 27 |
Globally, bigger is the data set, better is the array formula calculation speed up.
Multi thread calculation significantly improves performance. To enable multi thread calculation, follow these instructions. Finally, this excellent article contains everything you need to know to improve Excel performances.
Which interpolation method should I use ?
The choice of the interpolation methods depends on:
- The number of points
- The expected smoothness of the interpolation
- The performances (i.e. calculation speed)
Usually, while the data contains less than approximately 200 points, performances should not be an issue whatever is the selected interpolation method. To select an interpolation method, use the figure below. It shows the relative characteristics of interpolation methods in a smoothness vs calculation speed chart.
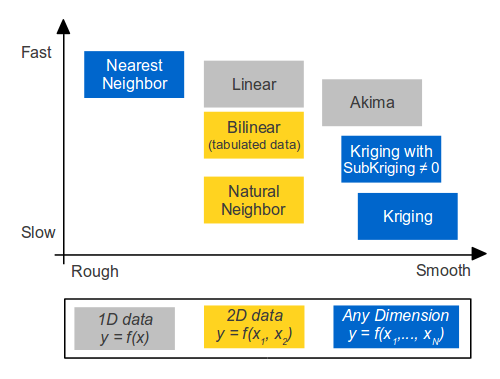
Interpolation Methods: smoothness vs calculation speed
What is the default add-in folder ?
Since Windows Vista and Excel 2007, it is %APPDATA%\Microsoft\AddIns. The following command should open this folder:
explorer.exe %APPDATA%\Microsoft\AddIns
How to update the Add-in ?
Open the add-in loader called INSTALL-XLL and click on the «Reinstall or update xll» button.
Or, replace .xll and .chm files in the add-in folder.
How to uninstall the Add-in ?
Open the add-in loader called INSTALL-XLL and click on the «Uninstall xll» button.
Or, delete .xll and .chm files in the add-in folder.
Why the blue help link does not work ?
.xll and .chm files must be stored in the same folder.